Mathematics is the language of the universe, but it’s a language few of us speak well. Yet mathematicians can use this language to help people better understand the world, discover unexpected connections and create new technologies. I talked to four UC Davis mathematicians about the problems they work on and why they are important. From quantum computers to the movement of subatomic particles and microorganisms swimming through fluids, it’s a journey that takes in ancient Greece, the lining of your lungs, lots of knots, dead ends in 19th century physics and artificial intelligence.
Mathematics competes with astronomy as our oldest science: Problems that ancient Greeks puzzled over are still being worked on today. Some ideas in math come from pure abstraction, but turn out to have unexpected connections to the real world; in other cases, an idea or concept from another field creates a whole new field of mathematics.

How tiny things swim through your body
Associate Professor Becca Thomases jokes that she’s an “accidental mathematician” who didn’t set out to be a professor.
“I just kept going in this direction and the research got more and more interesting and here I am,” she said.
Ignore the self-deprecation. Thomases’ work is showing how very small creatures move around and how your lungs function.
About four or five years ago, Thomases started looking at how microorganisms swim in fluids other than water.
In classical, Newtonian physics, fluids take the shape of their container while solids retain a rigid shape. There’s a well-known set of equations, the Navier-Stokes equations written about 300 years ago, which describe the forces acting when you move objects through classical fluids.
But in the real world, most materials have properties that lie somewhat in between. Push against a memory foam pillow or some mucus, and it will retain the impression then slowly “forget” it. These viscoelastic materials can store energy and release it over time.
“There’s a non-linear relationship between how you push on something and how it reacts,” Thomases said. “There’s no one model.”
Many microorganisms live in such fluids and our bodies are full of them — blood, mucus and lymph, to name a few. In our lungs and airways, tiny hairs called cilia work to keep mucus flowing up and out.
Thomases’ recent work shows the forces that act on these cilia as they poke into the mucus, push it in one direction then duck on the return stroke. This movement is essential to keeping our lungs healthy, she said.
She has also studied the mathematics of how microorganisms swim. Chlamydomonas is a single-cell green alga that propels itself with two whiplike hairs, or flagella. In water, Chlamydomonas moves with a sort of breast-stroke action. Because it’s so small, it has almost no inertia and so can’t “coast” on the effort of previous strokes. Thomases and Professor Bob Guy, also in the Department of Mathematics, modeled Chlamydomonas’ swimming in fluids of different viscoelasticity and showed that it should change stroke in more viscous fluids — a prediction borne out by observations.

“I definitely feel that I sit in the middle of the mathematicians, the engineers who want to use these tools, and the computational people writing the algorithms,” she said. “I’m able to translate those communities for each other.”
Which might be a good description of mathematics as a whole: still at the center, underlying all these different fields – physics, engineering, biology, computing — and bringing them together.

Knots and tangles and subatomic particles
Eugene Gorskiy’s office in the UC Davis math building is almost completely bare, except for the large whiteboard covered in equations in dry-erase red, green and blue. His work, however, is a little messier — Gorskiy is an associate professor in the tangled field of knot theory.
We’re all familiar with knots in shoelaces, neckties and headphone cables. They are also relevant to biology: DNA is a very long, thin molecule, and controlling how it gets knotted up or untangled is vitally important for life to function.
To a mathematician, knots are curves in space that may cross over each other a number of times, Gorskiy said. For any knot, mathematicians can calculate a set of numbers that describe it, called an invariant. If two knots have the same invariant, then they are essentially the same knot.
“You can deform it or pull strings out, but it’s still the same knot,” he said. “You can’t untie it just by stretching it.”
The simplest possible knot, mathematically, is a circle: it has an invariant of zero. Mathematicians studying knots want to work out how knots can be tied (by crossing over) or untied (how many crossings need to be removed to untangle them) and how to describe them.
Gorskiy became interested in knot theory during his doctoral work at Moscow State University. He was studying algebraic geometry — which deals with curves and parabolas — and noticed that some of the tools from geometry could apply to knot theory.
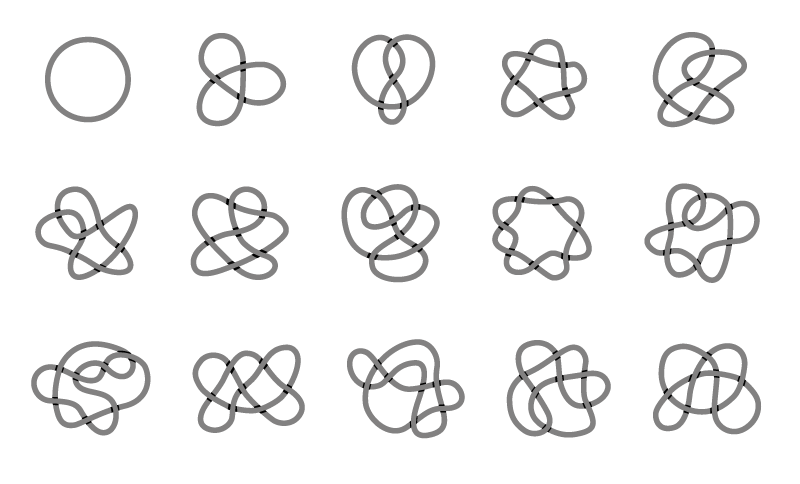
“Sometimes these algebraic tools allow you to get useful information about knots, and knot theory can give you a new perspective on algebra,” he said. “The most compelling thing for me is how you can connect these two different fields.”
Knot theory as a mathematical specialty originated in the late 19th century with the British scientist Lord Kelvin, Gorskiy said. Kelvin proposed that atoms were knots in the ether, a substance that, at the time, was thought to fill empty space. The properties of different elements, Kelvin theorized, would come from different types of knot.
As an idea about atomic structure, this would quickly turn out to be completely wrong, but it did lead mathematicians and physicists to start classifying and describing different kinds of knots and how they relate to each other. The field has been expanding ever since.
Yet over a hundred years later, knot theory is once again connecting to particle physics. Subatomic particles weave around each other as they move through space and time. The tracks of their movements can be described as mathematical knots and give information about the particles and how they relate to each other, Gorskiy said.

Helping machines make sense of data
Associate Professor Luis Rademacher is an applied mathematician interested in separating signals from a large mass of data. Rademacher’s interest is in artificial intelligence — specifically, how you can get machines to make sense of data. His goal is to develop basic tools, securely founded in theoretical math, that can be used to manage data.
“The tools have to be both well-founded in math and practical in application,” he said.
Rademacher is especially interested in problems of signal separation. Imagine a room full of people at a noisy cocktail party. Microphones placed around the room pick up the chatter, but how do you separate the general noise into different conversations, or signals? This general idea applies to a number of other examples such as interpreting magnetic signals in brain scans.
“There are many other problems that look like this after you stare at them for a while,” Rademacher said.
Rademacher has found that signal separation problems are affected by something he calls “the blessing of dimensionality.” Generally speaking, when you add dimensions — or attributes — to a problem, it gets more complicated to solve. To generalize, if you double the types of measurements considered, your problem gets about four times as complicated. Mathematicians call this “the curse of dimensionality.”
But in some cases, things actually get easier when you add more dimensions to your analysis, and the “curse” becomes the “blessing.”
Intuitively, this makes sense: It would be hard to distinguish people’s faces based on one characteristic, such as the distance between their eyes, but if you can consider other measurements as well, facial recognition gets much easier.
“If you look at more parameters you have more space to explore and more ways in which the data can look different,” Rademacher said. “But this only works if you have infinite computational power to work with.”
More data is better in a theoretical sense, but not necessarily in a computational sense, he said.
Rademacher picks problems based on whether he can make a practical difference, he said.
“Here are things I know I can do something about,” he said.

From ancient Greece to quantum computers
Ancient Greek mathematicians knew about the existence of prime numbers — whole numbers greater than 1 that are divisible only by 1 and themselves, such as 3, 19 or 7,753. But while modern mathematicians have calculated staggeringly large primes, we still don’t understand if there is some underlying structure or pattern to how they appear in the number line. It’s a problem that continues to plague the field of number theory — the mathematics of whole numbers — today.
“One thing I love about number theory is that it’s a really old field. The questions are easy to explain but the solutions are really complicated,” said Associate Professor of mathematics Elena Fuchs.
For the last few years, Fuchs’ special interest has been another ancient Greek puzzle, Apollonian circle packing. Around 200 BCE, Apollonius of Perga was drawing circles with a compass and ruler. He showed that if he drew three circles touching each other, there were only two ways to draw a line (or circle) that touched all three circles — a large circle outside, or a small circle in the middle of the other three.
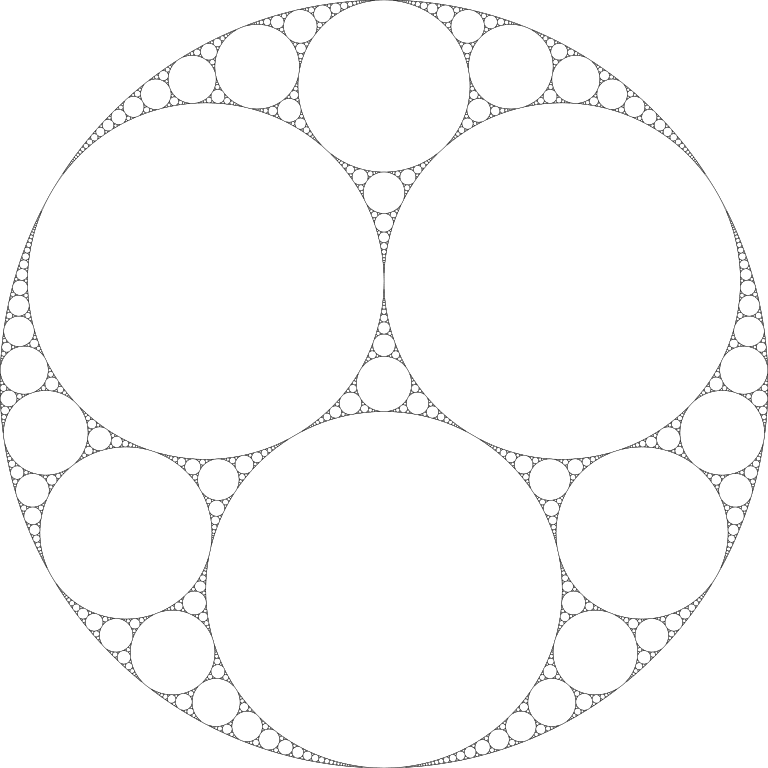
Over the centuries, many famous mathematicians have tinkered with these circle packing problems. In 1643, the French philosopher and scientist René Descartes discovered patterns in the size of circles in an Apollonian packing; Gottfried Liebniz also worked on them.
The size of circles is represented by their curvature, which is 1/radius of the circle. Therefore, the bigger a circle is (the higher the radius) the smaller the curvature. In the early 20th century, Frederick Soddy, 1921 Nobel laureate in chemistry, discovered that if the first three or four circles have curvature that is a whole number (or integer), every circle in the series will have whole-number curvature.
In other words, an infinite series of whole numbers emerges from this particular arrangement of circles.
“As number theorists, we get really excited about this sort of thing,” Fuchs said. “We want to ask questions such as, ‘are there prime numbers in the series and if so where?’”
The early 2000s saw a fresh explosion of interest in Apollonian circle packings, including Fuchs’ own work, which has connected the problem to other mathematical objects through something called Thin Group Symmetry. And this connection might lead to a whole new kind of computer — the quantum computer.
Digital devices handle data as bits that can be either one or zero. Quantum computers use qubits that can be one and zero simultaneously, thanks to the rules of quantum mechanics. Such computers should be extremely fast at addressing some types of problems, including calculating prime numbers and cracking encrypted data.
Thin Group Symmetry might be a candidate for the building blocks of quantum computers, Fuchs said.
“This is exactly what I love about number theory — there are all sorts of connections to other fields and you can go from really simple to really deep very quickly,” she said.
To explain the role of mathematics, Fuchs cites Andrew Wiles, the mathematician who proved Fermat’s Last Theorem after almost 350 years:
“You’re in a dark room with a bunch of furniture and you’re kind of feeling around with your hands trying to figure out what’s there, and suddenly you find a light switch and you see everything as it has been the whole time. I think that’s a really accurate description.”

Media contact: Andy Fell, News and Media Relations, 530-752-4533, ahfell@ucdavis.edu
Related Stories

Refugees Reclaim Human Rights With Technology
“In the whole world, if you are Syrian, you have nothing. You have no rights. You have no life,” Kaysaneya said, in English. “I lived a life, and it’s not the one I was dreaming about.”
From Molecules to Minds
Vastly more advanced than any supercomputer, the complexity and versatility of the human brain is awe-inspiring. How do we map the mind?

Researchers Have Forged a Path from UC Davis to Space
NASA has invested millions of dollars in UC Davis research, working with UC Davis biologists, engineers, physiologists, psychologists and other researchers to study life in space.

Pavement Research Center Keeps California on Road
Tough commute? Imagine driving it on roads of dirt or gravel.
