Quick Summary
- Math can be used to study knots and tangles in DNA
- Computer model shows how bacteria separate linked chromosomes
- Implications in biology, math, physics
If you’ve ever tried to untangle a pair of earbuds, you’ll understand how loops and cords can get twisted up. DNA can get tangled in the same way, and in some cases, has to be cut and reconnected to resolve the knots. Now a team of mathematicians, biologists and computer scientists has unraveled how E. coli bacteria can unlink tangled DNA by a local reconnection process. The math behind the research, recently published in Scientific Reports, could have implications far beyond biology.
E. coli bacteria can cause intestinal disease, but they are also laboratory workhorses. E. coli’s genome is a single circle of double-stranded DNA. Before an E. coli cell divides, that circle is copied. Opening up the double helix to copy it throws twisting strains elsewhere down the molecule — just as uncoiling a cord in one place will make it over-coil somewhere else. The process results in two twisted loops of DNA that pass through each other like a “magic rings” trick.
To separate the rings, E. coli uses an enzyme called topoisomerase IV, which precisely cuts a DNA segment, allows the loops to pass through the break and then reseals the break. Because topoisomerase IV is so important to bacteria, it’s a tempting target for antibiotics such as ciprofloxacin. But when topoisomerase IV is absent, another enzyme complex can step in to carry out this unlinking, although less efficiently. This complex introduces two breaks and unlinks by reconnecting the four loose ends.
“There are other ways to unlink the rings, but how do they do it?” said Mariel Vazquez, professor of mathematics and of microbiology and molecular genetics at the University of California, Davis.
One pathway, Vazquez said, is that the reconnection enzymes remove one link at a time until they get to zero. That solution was favored by the biologists.
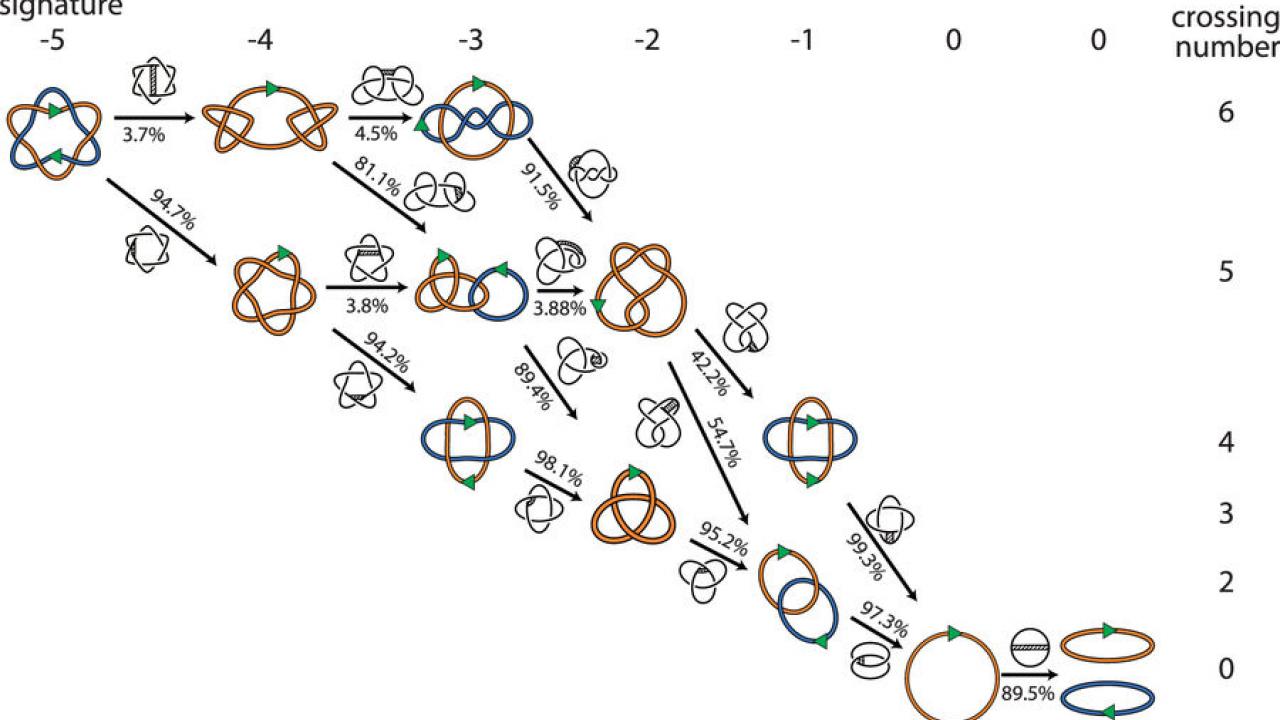
But mathematicians look at the problem slightly differently. They understand the DNA as a flexible curve in three-dimensional space. Certain points on the curve can be broken and reconnected. To a mathematician, there are many potential routes for reconnection processes to work — including some where the number of links actually goes up before going back down.
“These are all the same to a mathematician, but not to a biologist,” Vazquez said. To determine the most likely route and resolve the problem, they turned to computational modeling.
Vazquez and colleagues developed computer software with DNA represented as flexible chains to model the possible locations where reconnection enzymes could cut and reconnect the chains. Overall, they modeled millions of configurations representing 881 different topologies, or mathematical shapes, and identified hundreds of minimal pathways to get two DNA circles linked in up to nine places down to two separate circles.
The computer model confirmed the biologists’ hunch: Undoing one link at a time is the preferred route to separate the circles of DNA.
The results could have implications far beyond DNA biology, Vazquez said. There are other examples in nature of objects that collide, break and reconnect — like the dynamics of linked fluid vortices, or the patterns formed by smoke rings, for example. When solar flares are ejected from the sun, powerful magnetic field lines cross and reconnect.
“The math is not DNA specific, and the computation can be adapted,” Vazquez said.
Co-authors on the paper are: at UC Davis, Robert Stolz and Michelle Flanner; Masaaki Yoshida and Koya Shimokawa, Saitama University, Japan; Reuben Brasher, Microsoft, San Francisco; Kai Ishihara, Yamaguchi University, Japan; and David Sherratt, University of Oxford, U.K. The work at UC Davis was supported by the National Science Foundation, National Institutes of Health, Japan Society for the Promotion of Science and The Wellcome Trust.
Listen to this story on our podcast, Three Minute Egghead
Media Resources
Andy Fell, UC Davis News and Media Relations, 530-752-4533, ahfell@ucdavis.edu
Mariel Vazquez, Mathematics, mariel@math.ucdavis.edu